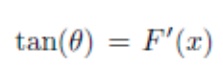We did it together!!! Through our mirror system, we demonstrated that multiple mirror surfaces can be combined to image a wider field of view using only calculus level math. So, before partying it up, we should show our gratitude to everyone who enabled us to participate in this research.
Special thanks to Dr. Emek Kose for being an amazing mentor; without her support and teaching, this research would have been an immensely difficult task. Also, many thanks to St. Mary's College of Maryland for hosting this Emerging Scholars Program--Research Experience for Undergraduates (ESP-REU). Last but not least, thanks to the National Science Foundation for funding our research under DMS-1005046 grant.
Mirror, Mirror, on the Wall, Which is the Clearest of Them All?
Thursday, July 19, 2012
The Miracle
This is the last push. Are you guys ready? If you answer is yes, you're a champ and if you're answer is no, let's just pretend you never said that.
As you remember, the goal of our research was to create a mirror that would image close to 180 degree field of view with minimum distortion. So for, we have looked at single mirror, and various 2-mirror combinations, but we strongly suspect that the answer lies in a 3-mirror combination. We learned that the rectifying mirror is great for reflecting the floor with minimum distortion. So the rectifying mirror is the permanent member of our mirror combination. We also learned that the forward looking mirror did a great job for reflecting the ceiling. So, only if we could rotate the forward looking mirror to reflect the surrounding wall, instead of the ceiling, it would be superb. But, if you go back and read the section on the forward looking mirror again, you'll remember that the forward looking mirror only works when the light rays are parallel to its optical axis. Therefore, we need a 45 degree linear mirror to not only change the path of light and hit the forward looking mirror, but to make sure that the light rays would hit the forward looking mirror parallel to the x-axis.
But these are all nice theories. Do they really work as we want them in reality? Let's see!
We will first start with the rectifying mirror. From our research and testing of the rectifying mirror in Pov-Ray, we identified the rectifying mirror as being optimal for imaging the floor of our test room. Sorry for the repetition. JUst making sure everyone is on the same page as us. Because the rectifying mirror is good at imaging the floor, it will be the foundation for which we add the other mirrors. In Maple we started the numerically solved rectifying mirror on the positive side of the x -axis so that it could be rotated symmerytrically in Pov-Ray. We then gave the rectifying mirror the initial conditions y(0)=1 and set the x- coordinates range to be (x=0.0001..0.70). For the rest of our research the rectifying mirror remained at this fixed point.
To brigde the gap between the rectifying and forward looking mirror, we added a linear mirror using the equation of a line y=mx+b. The linear mirror was put in between the two mirrors to direct the light rays from the image plane parallel to the forward looking mirror where the light ray will travel a third time back to the image plane. We ensured that the lightrays leaving the image plane after hiting the linear mirror were exactly parallel to the forward looking mirror by giving the line a 45 degree angle slope meaning we used the line equation y=x. To connect all three mirrors, we kept m=1, but ajusted the b from the equation y=mx+b accordingly to test the design. In our final combination we found the equation for our linear mirror to be y=x+0.42155 and the length was 0.15 units given by the range x=0.70..0.85. Through trail and error we realized that the linear mirror worked better at a shorter length, but if it was too short it would not direct enought light rays to the forward looking mirror.
The third mirror that ended that completed the design of our catadipotric sensor was the forward looking mirror. For our catadoptric sensor we used the forward looking mirror to help with imaging the wall and recieving the light rays directed by the linear mirror. Since the light rays traveling from the linear mirror to the forward looking mirror are parallel to the x-axis, we solved our equation for the function of the forward looking mirror in terms of y. Similar to the computations perviously done for the forward looking mirror, we used the vector method to find F(y). we're not gonna bore you with the excruciating math steps that we have already gone over in previous posts.
So, we went a little bit overboard with our explanation. But, we can't help it. Once we start talking about math, it's hard to get us to stop. All we want to say is that we are very excited. This combination of the rectifying, the 45 degree linear and the forward looking mirror works. And we found this combination for the first time. It had never been obtained before. We capture approximately 160 degree field of view since the remaining of our field of view is blocked by the forward looking mirror. And here is the doozy, we have minimum distortion in our design. Just keep in mind that small rings that you see in our Pov-ray picture it has to do with Pov-ray itself and not our design! But, the circle in the floor it's just a gap between our mirrors.
Wednesday, July 18, 2012
2-mirror combinations
We've got to that point in our research, where we can do our own thing and be creative, while having our goal in mind. I guess it's worth mentioning our goal again. We are trying to obtain an ultra wide field of view with minimum/no distortion. Awesome, so let's get to work by which, of course, I mean let's combine any two mirror that we have been introduced to you in the past couple of weeks.
(1): The first 2-mirror combination that we looked at was a combination of the rectifying with the panoramic mirror. we know that the rectifying mirror has an outstanding record for imaging the floor with the minimal distortion that is all lines are mapped to lines. We also remember that the panoramic mirror otherwise known as the wall-mirror could be used for imaging the surrounding walls. So, by combining these two mirrors we should be able to image the floor and the surrounding wall and achieve an ultra field of view.
In order to achieve the above combination of mirrors, we find the point of intersection between the graphs of panoramic and rectifying mirror (we showed how to obtain the graphs of these mirrors in the previous posts). We cut the panoramic mirror before the point of intersection, so that we only have the rectifying mirror at first. Then, after the intersection point, the rectifying mirror is cut so that there is only panoramic mirror. In this manner, as the object moves from the floor to the walls, we image a hemisphere. However, the farther we get from the center to the walls, the greater the distortion and the results are not satisfactory.
(2): The second mirror combination that we experimented with is the rectifying mirror and a linear mirror. The steps in this experiment identical to the first case. However, in this case, the linear mirror only changes the path of light and has no impact on the field of view and is therefore unhelpful.
(3): The third case involved combining the rectifying mirror with good old parabolic mirror. Surely you have noticed that all three of these cases have a rectifying mirror in their combination and the underlying reason for choice of mirror is that we have seen through our calculations and experiments that the rectifying mirror provides a perfect image of the floor plane. Therefore, in our combinations we are just looking for a second mirror that increases our field of view to approximately 180 degree with minimum distortion. We considered using parabolic mirror in this combination because of its focal properties. If you remember, in a parabolic mirror the light rays will always pass through its focus point. However, the image is very distorted in this case! The equation of the parabolic mirror used here is:
Forward Looking Mirror
It's time to learn about another type of mirrors. we've come a long way from a rectifying mirror to a parabolic, panoramic and now to forward looking mirror. Good job everyone!
As the name forward looking suggests, it reflects a plane directly above its optical axis. Forward looking mirror only works under orthographic projection, where the light rays travel parallel to the mirror's optical axis.
As explained above, the forward looking mirror reflects a plane above its optical axis such as the plane y=k, where our object is positioned. In other words, the object in on the ceiling.
Suppose the incoming and outgoing light rays are vectors u and v, respectively. We also know that the normal line n is a vector. Therefore, we use vector method to find an equation for our forward looking mirror.
The first step in solving this problem is to normalize our vectors, by finding a new vector in the same direction as our vectors u and v but in terms of their unit length. In order to do so, we need to find the position vectors of u and v by subtracting their terminal point from their initial point. Then we divide each position vector by its magnitude using the pythagorean theorem.
Using the infinity trick that we used previously with the panoramic mirror helps simplifying the math for normalizing vector v.
We Add together the two normalized vectors u and v by creating a parallelogram. The sum of these two vectors will be parallel to vector n. We know that parallel vectors have the same slope; thus the slope of the normal vector is the same as the slope of the sum of vectors u and v. Because normal and tangent lines are perpendicular to each other, the slope of n is negative and reciprocal of the slope of the tangent line. Now we know the slope of the tangent line and as a result we can find the equation of the mirror, as simple as that!
Please, don't be intimidated by all these math equations. We've taught you all the math you need to follow along with us, even if you're not a math person!
We solve the non-linear ordinary differential equation numerically in Maple, which enables us to graph the function of the mirror. To visualize the mirror we create a surface of revolution in Pov-ray by using the points obtained in maple.
Just as a general reminder, the green and black checkers demonstrate the ceiling, while blue and white, red and white, red and black and blue and black are the four surrounding wall in the test room in Pov-ray.
Panoramic Mirror with Infinity Trick
Not to sound lazy or anything but the numeric solution for the panoramic mirror in the last post was just too much work! That is why we tried to solve it analytically, this time.
So, we still have the same panoramic mirror as before, where the object is positioned on a surrounding wall with the coordinates (k, ax+b). The image plane is below the x-axis and is indicated by y=-k.
So, we still have the same panoramic mirror as before, where the object is positioned on a surrounding wall with the coordinates (k, ax+b). The image plane is below the x-axis and is indicated by y=-k.
But, here is the time to use a trick. We know that "a" is an arbitrary scaling factor and the bigger the "a", the bigger the field of view. Therefore, it shouldn't matter whether it is ax+b or kax+b or gax+b. "a", "ka" and/ or "ga" are all scaling factors. So, for the sake of our trick, let's say it is kax+b.
Now, once again, we draw the tangent line to the mirror at point (x, F(x)) and we have:
Using the tangent double-angle formula we have:
Here is where the trick comes into the picture. Suppose k is going to infinity and find the limit of tangent of 2theta:
It looks so cool, doesn't it?
By equating the (2) and the (4) equations, we get:
YAY! We got our differential equation. Now, by solving this differential equation in maple and finding the surface of revolution in Pov-ray we obtain the same results as we did previously :)
Thursday, June 28, 2012
Panoramic Mirror
More mirrors!!! Awesomeness!! This time we are back to mimic panoramic imaging. Panoramic imaging covers up to 360 degrees, this is while the approximated field of view of humans is 95 degrees out, 75 down, 60 in and 60 up!
As shown in the picture below, the panoramic mirror is surrounded by walls so far away from the optical axis of the mirror that the walls seem like a cylinder. This mirror reflects the image of an object positioned on the wall . In all the previous cases that we studies, the object was positioned on the floor. However, regardless of the position of the object, out goal remains the same. We want to find the equation of such mirror with orthographic projection.
We know that tangent of an angle is opposite over adjacent. Thus, we find the tangent of angle 2 theta as following:
Now, we can easily use double-angle identity,
By equating the two equations, we have a differential equation to solve in Maple based on x and a:
a is a scaling factor and the bigger the a, the bigger the field of view and less distortion.
1) a=1
2) a=500
3) a=1000
However, we tried to further reduce the distortion in the mirror by increasing a beyond 100, but we didn't notice any significant change in the distortion pass that point.
Monday, June 25, 2012
Minimum Distortion
As we experienced with spherical and parabloid mirrors, when the mirror is of a quadratic function, there is a great distortion in the image. In a study done by Andrew Hicks, University of Pennsylvania, it was found that when the distance between the object and the image plane is of a linear function, the image captured by a mirror in both perspective and orthographic projections has no distortion.
In the picture below, you're looking at an orthographic projection. From the Law of Reflection, we know, the angle of incidence = the angle of reflection = ϴ. From the paper we were given the
tan(ϴ )=F'(x) and we used the image plane, tangent line from the point on the mirror, and the parallel light ray to uderstand where the equation came from. In the picture, the angle between the normal line and tangent line is 90 degrees. To get the smaller angle for our traingle and solve for the unknown angle formed by the interesection of the image plane and tangent line, we identified the angle as (90-ϴ ). The angle formed from the interesection of the parallel line an the image plane was know to be 90 degrees. With this information from the picture, we go that ϴ was equal to our unknown angle, and the tan(ϴ) was equal to F'(x) because it represented the raise and run from the image plance to the point on the mirror containing F(x). Our was as follows
`
In the picture below, you're looking at an orthographic projection. From the Law of Reflection, we know, the angle of incidence = the angle of reflection = ϴ. From the paper we were given the
tan(ϴ )=F'(x) and we used the image plane, tangent line from the point on the mirror, and the parallel light ray to uderstand where the equation came from. In the picture, the angle between the normal line and tangent line is 90 degrees. To get the smaller angle for our traingle and solve for the unknown angle formed by the interesection of the image plane and tangent line, we identified the angle as (90-ϴ ). The angle formed from the interesection of the parallel line an the image plane was know to be 90 degrees. With this information from the picture, we go that ϴ was equal to our unknown angle, and the tan(ϴ) was equal to F'(x) because it represented the raise and run from the image plance to the point on the mirror containing F(x). Our was as follows
ORTHOGRAPHIC PROJECTION GRAPH
With the infromation from the picture, we used the double angle identity for the tan function to get 

We were then able to use Maple to put in the function and get an equation for F'(x). In the new form of an ordinary differentiable equation, we solve for F(x) using it's derivative F'(x). The equation for F(x) was the surface of our mirror with minimal distortion and we then graphed it in Maple to get a visual idea of what our discovered mirror surface looked like. THE END
FUNCTION OF A MIRROR SURFACE IN ORTHOGRAPHIC PROJECTION
Subscribe to:
Comments (Atom)